2022广东高考数学模拟试题及答案解析

2022广东高考数学模拟试题及答案解析

一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上）

1．复数

的共轭复数是

A．1﹣iB．1＋iC．﹣1﹣iD．﹣1＋i

2．已知集合M＝

，N＝

，则M

N＝

A．[﹣1，0]B．(0，1)C．[0，1]D．

3．已知抛物线C：

(p＞0)的准线为l，圆M：

与l相切，则p＝

A．1B．2C．3D．4

4．某学校组织学生参加数学测试，某班成绩的频

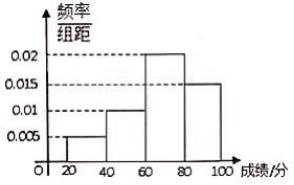
率分布直方图如下图，数据的分组依次为[20，

40)，[40，60)，[60，80)，[80，100]．若不低

于60分的人数是35人，则该班的学生人数是

A．45B．50

C．55D．60

5．中国古代数学名著《周髀算经》记载的“日月

历法”曰：“阴阳之数，日月之法，十九岁为一第4题

章，四章为一部，部七十六岁，二十部为一遂，遂千百五二十岁，…．生数皆终，万物复苏，天以更元作纪历”．某老年公寓住有20位老人，他们的年龄（都为正整数）之和恰好为一遂，其中最年长者的年龄大于90且不大于100，其余19人的年龄依次相差一岁，则最年长者的年龄为

A．94B．95C．96D．98

6．已知

(0，

)，

，则

＝

A．

B．

C．

D．

7．已知直三棱柱ABC—A1B1C1的6个顶点都在球O的球面上，若AB＝1，AC＝

，AB⊥AC，AA1＝4，则球O的表面积为

A．5

B．10

C．20

D．

8．对于定义在R上的函数

，

为偶函数．当x

(0，

)时，

，设

，

，

，a，b，c的大小关系为

A．a＜b＜cB．b＜c＜aC．b＜a＜cD．c＜a＜b

二、 多项选择题（本大题共4小题，每小题5分， 共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）

9．设a，b，c为正实数，且a＞b，则

A．

B．

C．

D．

10．已知曲线C1：y＝2sinx，C2：

，则

A．把C1上各点的横坐标缩短到原来的

倍，纵坐标不变，再把得到的曲线向左平行移动

个单位长度，得到曲线C2

B．把C1上各点的横坐标缩短到原来的

倍，级坐标不变，再把得到的曲线向右平行移动

个单位长度，得到曲线C2

C．把C1向左平行移动

个单位长度，再把得到的曲线上各点的横坐标缩短到原来的

倍，纵坐标不变，得到曲线C2

D．把C1向左平行移动

个单位长度，再把得到的曲线上各点的横坐标缩短到原来的

倍，纵坐标不变，得到曲线C2

11．若函数

对

a，b

R，同时满足：（1）当a＋b＝0时有

；（2）当a＋b＞0时有

，则称

为

函数．下列函数中是

函数的有

A．

B．

C．

D．

12．在长方体ABCD—A1B1C1D1中，M，P是平面DCC1D1内不同的两点，N，Q是平面ABCD内不同的两点，且M，P，N，Q

CD，E，F分别是线段MN，PQ的中点．则下列结论正确的是

A．若MN∥PQ，则EF∥CD

B．若E，F重合，则MP∥CD

C．若MN与PQ相交，且MP∥CD，则NQ可以与CD相交

D．若MN与PQ是异面直线，则EF不可能与CD平行

三、填空题（本大题共4小题， 每小题5分，共计20分．请把答案填写在答题卡相应位置上）

13．函数

的图象在点(1，

)处的切线方程为．

14．

的展开式中

的系数为（用数字填写答案）．

15．已知向量

＝(1，a)，

＝(2b﹣1，3)(a＞0，b＞0)，若

⊥

，则

的最小值为．

16．已知F1，F2是双曲线C：

(a＞0，b＞0)的左、右焦点，以F1F2为直径的圆与C的左支交于点A，AF2与C的右支交于点B，cos∠F1BF2＝

，则C的离心率为.

四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）

17．（本小题满分10分）

在①sinB＝

sinC，②b＝4sinA，③B＋C＝2A这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求c的值；若问题中的三角形不存在，说明理由．

问题：是否存在△ABC，它的内角A，B，C的对边分别为a，b，c，且4asinB＝

bcosA＋bsinA，a＝2，?

注：如果选择多个条件分别解答，按第一个解答计分．

18．（本小题满分12分）

设

是公比大于1的等比数列，

，且

是

，

的等差中项．

（1）求数列

的通项公式；

（2）若

，求数列

的前n项和

．

 

19．（本小题满分12分）

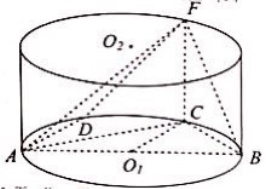
如图，在圆柱O1O2中，AB为圆O1的直径，C，D是弧

上的两个三等分点，CF是圆柱O1O2的母线．

（1）求证：CO1∥平面AFD；

（2）设AC＝

，∠FBC＝45°，求二面角B—AF—C的余弦值．

20．（本小题满分12分）

为了进一步提升广电网络质量，某市广电运营商从该市某社区随机抽取140名客户，对广电网络业务水平和服务水平的满意程度进行调查，其中业务水平的满意率为

，服务水平的满意率为

，对业务水平和服务水平都满意的有90名客户．

（1）完成下面2×2列联表，并分析是否有97.5%的把握认为业务水平与服务水平有关；

	对服务水平满意人数	对服务水 平不满意人数	合计
对业务水平满意人数
对业务水平不满意人数
合计

（2）为进一步提高服务质量，在选出的对服务水平不满意的客户中，抽取2名征求改进意见，用X表示对业务水平不满意的人数，求X的分布列与期望；

（3）若用频率代替概率，假定在业务服务协议终止时，对业务水平和服务水平两项都满意的客户流失率为5%，只对其中一项不满意的客户流失率为40%，对两项都不满意的客户流失率为75%，从该社区中任选4名客户，则在业务服务协议终止时至少有2名客户流失的概率为多少?

附：

P( )	0.10	0.05	0.025	0.010	0.005	0.001
	2.706	3.841	5.024	6.635	7.879	10.828

，其中

．

21．（本小题满分12分）

已知椭圆C的两个焦点分别是(﹣1，0)，(1，0)，并且经过点(1，

)．

（1）求椭圆C的标准方程；

（2）已知点Q(0，2)，若C上总存在两个点A、B关于直线y＝x＋m对称，且

，求实数m的取值范围．

 

 

22．（本小题满分12分）

已知函数

．

（1）讨论

的单调性；

（2）设

，函数

有两个不同的零点

，

(

＜

)，求实数a的取值范围．

2022广东高考数学模拟试题答案解析

·1·